![]()
www.heteroclinic.net
This problem is studied as part of Zhikai Wang's master research. The computation tool is AUTO. Under the direction of the supervisor and by extending AUTO demos, some results are obtained. For example the 1,024 heteroclinic connections for some specific parameter settings.
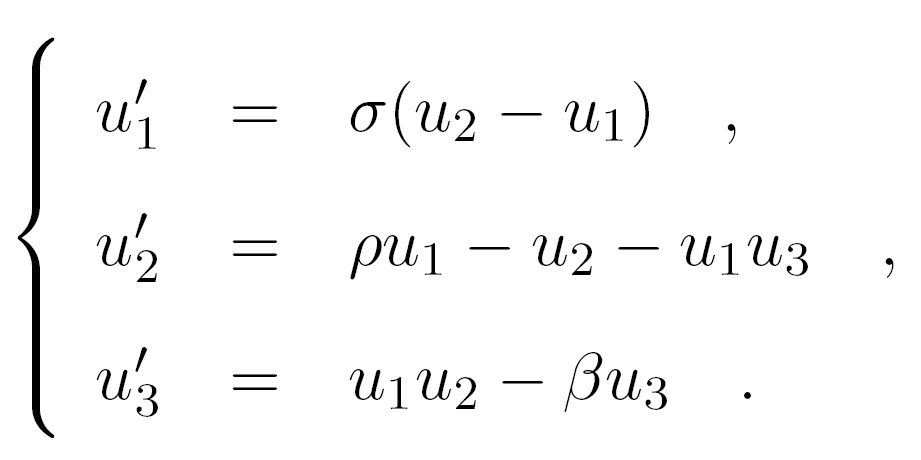
It gives a better sense of how a planar disc 'rolls' under the evolution laws. At the same time, we also see clearer the role that 'rho' plays.
Put two manifolds, rho=15 and rho=60, in the same scene.
The symbols sequence of heteroclinic connections, rho=28.
Does it show the Poincare sections of the unstable manifolds of the secondary equilibria? That reminds me `Zhou Yi', ``Taichi sheng liang yi...''.
Of course, there are numerous literatures for this problem.